Research on the Registration and Fusion Algorithm of Terahertz SAR Images

I.   Introduction

The terahertz (THZ) wave was widely investigated for its better transmission characteristics and the interference immunity than the optical waves. And it was less influenced by the solar radiance, thermal radiation and the particle distribution of the time varying atmosphere. The advantages of the terahertz radar over the microwaves radar were that the THZ radar bandwidth was wide, there was high resolution of the THZ images, and the THZ wave was more sensitivity to the Doppler shift. It represents a significant emerging technique in the domains of target detection, tracking, and identification with extensive application prospects in both military and civilian sectors. Recently, research areas like image processing based on terahertz SAR imaging and target recognition have gained considerable attention. However, due to the long wavelength of terahertz waves and limitations in hardware and software capabilities, images generated by terahertz imaging systems suffer from challenges including high noise levels, low contrast visibility, and substantial loss of edge information. Consequently improving the quality of terahertz SAR images has become a prominent focus of research.

The enhancement of terahertz radar SAR image quality can be achieved through two approaches, namely image processing and signal processing [1]-[3]. Enhancing SAR image quality through signal processing requires the acquisition of echo parameters, which often present challenges in terms of storage and computational complexity, resulting in significant costs in manpower and resources. As a result, publicly available SAR images are commonly utilized. Therefore, it is crucial to investigate image quality enhancement methods based on advanced image processing techniques [4]-[6].Image quality can be enhanced through advanced techniques such as super-resolution reconstruction or image fusion [7]-[9]. Due to the high level of noise and a low signal-to-noise ratio in terahertz SAR images, as well as the challenges associated with acquiring such images, only a limited number of researchers have explored methods for enhancing the quality of terahertz SAR images. Considering the unique characteristics of terahertz imagery, image fusion techniques are particularly suitable due to their ability to preserve complementary and redundant information from multiple sources, thereby improving image quality while simultaneously reducing noise levels [10]-[12]. Image registration is essential prior to the image fusion process [13]-[15]. The current registration methods primarily rely on the utilization of SIFT, SURF, and KAZE operators to extract feature points from diverse images [16]-[18].The Random Sample Consensus (RANSAC) algorithm is employed to filter feature points from different images, however, this approach often fails when dealing with high-noise images [19], [20]. The present article introduces an improved RANSAC algorithm that incorporates a feedforward preprocessing technique for the purpose of image registration and fusion.

The present study proposes an enhanced RANSAC algorithm with a forward preprocessing approach, based on SIFT, SURF, and KAZE operators, to achieve image registration and fusion in order to enhance the quality of terahertz SAR images. This research provides valuable support for target characterization analysis and recognition in terahertz SAR imagery.

II.   Theory

The presence of significant noise and the absence of texture information in terahertz image sequences impose limitations on their application in target feature extraction and intelligent recognition. Additionally, due to antenna aperture constraints, only a small central portion of the image contains valid information. Therefore, it is imperative to investigate techniques for terahertz image registration and fusion to enhance practicality while reducing image noise.

The THZ image as the Figure 1 exhibits a low signal-to-noise ratio and is further constrained by the antenna aperture, resulting in only a small central section of the image containing valid information. This poses challenges for image registration and fusion.

Figure  1.  Adjacent frame terahertz images a₁). The first frame of the first group a₂). The second frame of the first group b₁). The first frame of the second group b₂). The second frame of the second group.

DownLoad: Full-Size Img PowerPoint

1   Image registration

Image registration plays a pivotal role in enhancing image quality and facilitating image fusion, serving as the fundamental basis for this process. This study explores a corner point matching-based algorithm for image registration.

1   Feature detection

The invariance of feature keypoints under different scales and rotations is a crucial property. Feature point detection algorithms aim to capture the stable characteristics of an image by identifying local extrema points, which are subsequently utilized for feature matching across various images [21]. This study investigates the extraction and registration of typical feature points such as SIFT, SURF, and KAZE.

The SIFT algorithm is a feature extraction technique based on scale space. It applies Gaussian filters to the original image at multiple scales in order to extract key points, their corresponding scales and orientations, as well as feature vectors. The extracted feature operators can be utilized for image registration.

The scale space of an image $I(x,y)$ at different scales can be represented by convolving the image with a Gaussian kernel:

$G(x,y,\sigma )$ is a scale-variable Gaussian function, represents the scale-space factor, and $(x,y)$ is the pixel position of the image.

The scale variation feature is overcome by subtracting the adjacent upper and lower layer images in the scale space, which results in a Gaussian difference pyramid (DoG pyramid). This process effectively captures the contour features of the target:

the scale difference $k$ represents the ratio between two consecutive levels.

The local extreme position, which corresponds to the keypoint location and its corresponding scale, is obtained by comparing each pixel in the DoG scale space with its surrounding 8 pixels within the same layer, as well as 18 pixels from the upper and lower layers. To eliminate initially searched unstable feature points, methods such as curve fitting are employed due to the possible presence of weak contrast or strong edge respon、se among candidate feature points. After identifying the feature points, their directions are determined using gradient functions. Statistical analysis of gradient values and direction information around each feature point is then conducted to calculate both angle $m$ and magnitude $\theta$ of gradients:

The SURF algorithm is an enhanced version of the SIFT algorithm, utilizing the Hessian matrix for detecting extrema points and extracting local features. It streamlines the Gaussian template, resulting in expedited feature extraction and matching speed as well as fortified robustness.

For an image $I$ and a certain pixel point $X = (x,y)$, the Hessian matrix at scale is defined as:

The variable ${L_{xx}}(X,\sigma )$, ${L_{xy}}(X,\sigma )$, ${L_{yy}}(X,\sigma )$represents the convolution of image $I$at point $(x,y)$ with the second-order Gaussian derivative ${\partial ^2}\left[ {g(\sigma )} \right]/\partial {x^2}$, ${\partial ^2}\left[ {g(\sigma )} \right]/\left( {\partial x\partial y} \right)$ and ${\partial ^2}\left[ {g(\sigma )} \right]/\partial {y^2}$. $g(\sigma )$ is the probability density function of the Gaussian distribution.

The SURF algorithm constructs a scale space by employing box filters of varying sizes. To compensate for the introduced approximation error resulting from the utilization of box filters, it becomes imperative to multiply ${L_{xy}}$ by a weighting factor of 0.9 in order to rectify the discrepancy. The expression is as follows:

After establishing the scale space, the pixel extrema of this scale space can be obtained by approximating the Hessian matrix. These extrema are compared with 26 neighboring pixels in adjacent scale spaces to determine a set of feature points using non-maximum suppression. Finally, a Taylor expansion is applied to the Hessian matrix to eliminate low-contrast feature points from the set.

The KAZE algorithm is an adaptive feature extraction technique based on a nonlinear scale space that exhibits invariance to variations such as rotation, scaling, and illumination. It can effectively extract a larger number of feature points to enhance the registration effect.

The KAZE algorithm constructs a pyramid-shaped nonlinear scale space using the variable conductance diffusion method and the additive operator splitting algorithm (AOS), similar to building a Gaussian pyramid with SIFT.

Figure  2.  RANSAC algorithm with feedforward preprocessing

DownLoad: Full-Size Img PowerPoint

Since nonlinear diffusion filtering is performed in terms of time units, it becomes necessary to convert the scale parameter into time units:

The total number of layers in the pyramid is represented by $N$.

The nonlinear scale space of image $I$ can be obtained after applying the AOS algorithm:

The formula represents the image after undergoing Gaussian filtering, where $L$ denotes the resulting image, $i \in \left[ {0,N - 1} \right]$,$t$ represents time, and ${A_l}({L^i})$ signifies the conductivity matrix in multiple dimensions.

After constructing a nonlinear scale space, each point is compared with the pixel grayscale values in the surrounding $3 \times 3$ neighborhood as well as two layers of spatial information above and below to identify local maxima points of the Hessian matrix as feature points. The formula for calculating the Hessian matrix remains unchanged:

After detecting the position of feature points, the precise location of these points is determined through Taylor expansion.

2   Feature matching algorithm

The THZ images collected in this article exhibit significant noise and a lack of texture information. The feature points obtained through coarse registration are typically disordered, while the correctly registered points are often sparse, with significantly fewer numbers compared to the incorrectly matched points. Image registration presents an exceptionally challenging task. Therefore, based on features with minimal variation in aircraft trajectory, this article proposes an enhanced RANSAC algorithm that incorporates slope consistency and integrates pre-processing of matching point pairs.

Figure  3.  Mask. a₁) first frame mask of the first group a₂) second frame mask of the first group b₁) mask in the first frame image of the first group. b₂) mask in the second frame image of the first group. c₁) first frame mask of the second group c₂) second frame mask of the second group d₁) mask in the first frame image of the second group. d₂) mask in the second frame image of the second group.

DownLoad: Full-Size Img PowerPoint

Step 1. The image deflection angle for measuring THZ images of the aircraft is set within a range of ±10 degrees, as there were no abrupt changes in direction observed, $\theta = 20^\circ$.

Step 2. The direction angles of matching point pairs should be arranged and classified based on the consistency of slopes. Begin with an initial value n=1, and divide them into intervals. If there are only a few points within the interval, proceed to step 4; otherwise, move on to step 3.

Step 3. Random Sample Consensus algorithm (RANSAC) is utilized to eliminate outliers in the matching points and compute the positional error of the matches. Subsequently, proceed to step 2 and progressively narrow down the range of angular directions until the calculated error E falls below a specified threshold value.

The matching point in the second frame image is denoted as B_i, while A_i represents the matching point in the first frame image. The registration matrix TM is obtained through least squares using A_i and B_i.

Step 4. The coarse tentative matching pairs are successively reduced based on the RANSAC algorithm principle until the minimization of calculation error E is achieved.

3   Image registration measurement

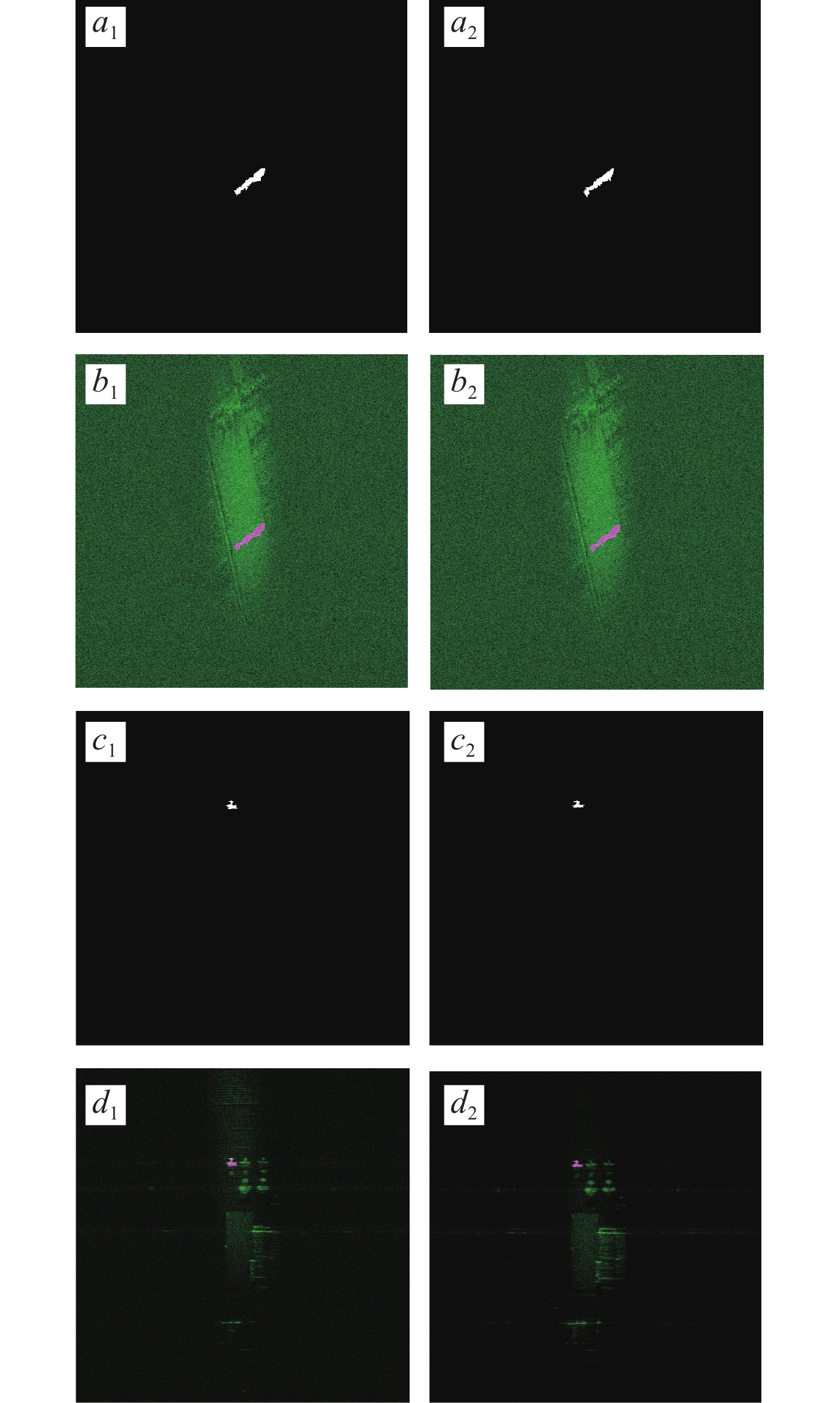
The quality of image registration in different frames is assessed by employing a fixed reference object within the same scene.

A clustering algorithm is used to extract stationary objects from various frame images, and masks are generated as the figure 3. The degree of overlap between these masks serves as an evaluation metric for assessing image registration quality and comparing the accuracy of different registration methods.

The registration accuracy is quantified by the mask overlap rate, denoted as P, in accordance with the subsequent formula:

The areas ${S_A}$ and ${S_B}$ represent the respective coverage of distinct frame image masks, while ${S_A} \cap {S_B}$ denotes their overlapping region.

2   Image fusion

Image fusion serves as a crucial technique for enhancing image quality, as it effectively mitigates image noise while simultaneously incorporating valuable information into the images.

1   Image fusion method

The present article employs a weighted image fusion method to effectively eliminate stitching gaps by utilizing the average grayscale value of overlapping region pixels for seamless image integration.

The grayscale values of F1 and F2 represent two frames of images, while the grayscale value of F corresponds to the fused image. The coordinates (x, y) indicate the pixel location associated with the respective grayscale value.

2   Image fusion effect evaluation

This article utilizes the grayscale normalized standard deviation of the overlapping region mask in fused images as a metric for quantifying the denoising effect. Furthermore, image entropy is employed to assess the level of information richness present in these fused images.

The normalized standard deviation D of the gray level in the overlapping region of the mask can be expressed as follows:

The variable $Mask$ represents the intersection area between the mask of the first frame image and the registered mask of the second frame. N denotes the total number of pixels within the mask, while Fi indicates the grayscale value of the image.

The original text states that the dielectric constant of the fixed reference object surface in the image is assumed to be uniform, with a consistent grayscale value represented by the average grayscale. A smaller standard deviation indicates reduced image noise.

The image entropy EN is commonly utilized as a metric for quantifying the information content within an image. A higher value of image entropy indicates that the image retains more comprehensive information, resulting in enhanced clarity.

The variable a represents the grayscale value of an image, whereas ${P_A}(a)$ denotes the probability distribution function of grayscale.

III.   Results and Analysis

The SIFT, SURF, and KAZE algorithms were used in this article for image registration

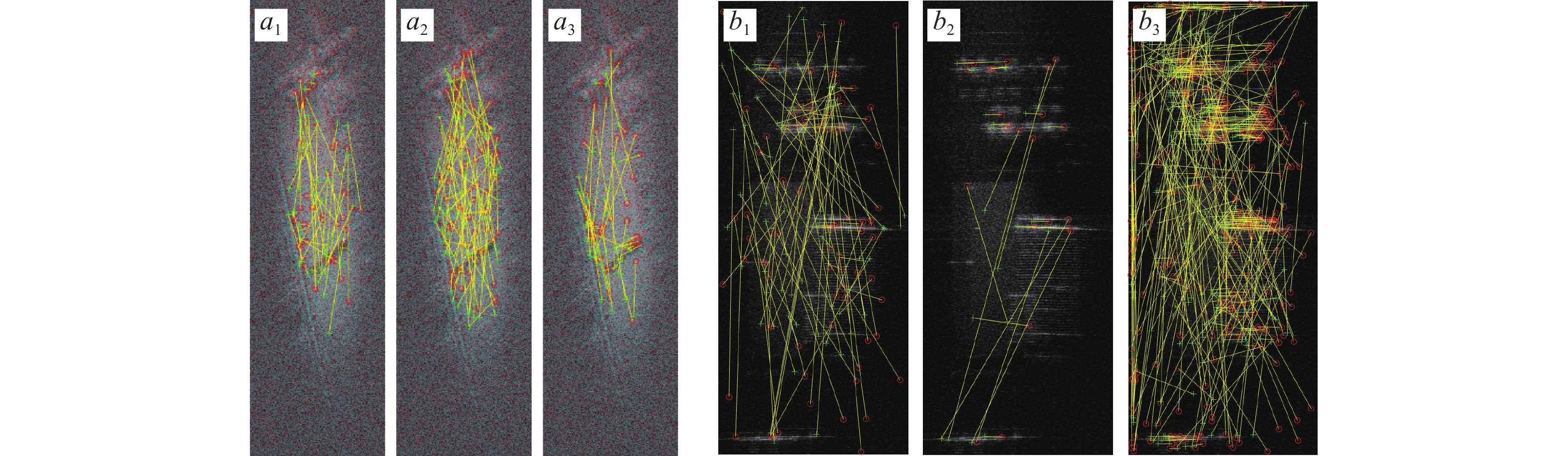
The THZ images exhibit uneven noise with significant fluctuations, and their lack of texture features as depicted in Figure 4 results in an irregular distribution of directional matches for corner points, posing challenges for image matching. Coarse registration results obtained using SIFT, SURF, and KAZE operators for corner point extraction are shown in Figure 5, where only a few pairs of correctly matched corner points are identified. However, algorithms such as BRISK, MSER, and ORB fail to achieve coarse registration as they struggle to extract any usable corner points. Directly applying the RANSAC algorithm to eliminate inconsistent matches from the coarsely registered corner points extracted by SIFT, SURF and KAZE algorithms as illustrated in Figure 6 does not yield accurate registration due to a significantly larger number of incorrect matches compared to correct ones. The data lacks consistency and cannot be directly utilized for precise image alignment using the RANSAC algorithm. Therefore, preprocessing and filtering of feature point matches in the image is necessary. Since the edge signal information in the image is insufficiently clear and for better visualization purposes, the following figures display cropped versions of the original image.

Figure  4.  Original images. a₁) first frame image of the first group a₂) second frame image of the first group a₃) mask in the original images of the first group b₁) first frame image of the second group b₂) second frame image of the second group b₃) mask in the original images of the second group

DownLoad: Full-Size Img PowerPoint

Figure  5.  Coarse registration regarding two groups. a₁) SIFT registration of the first group images a₂) SURF registration of the first group images a₃) KAZE registration of the first group images b₁) SIFT registration of the second group images b₂) SURF registration of the second group images b₃) KAZE registration of the second group images.

DownLoad: Full-Size Img PowerPoint

Figure  6.  RANSAC regarding two groups. a₁) SIFT registration of the first group images a₂) SURF registration of the first group images a₃) KAZE registration of the first group images b₁) SIFT registration of the second group images b₂) SURF registration of the second group images b₃) KAZE registration of the second group images.

DownLoad: Full-Size Img PowerPoint

The registration results obtained using an improved RANSAC algorithm with preprocessing are depicted in Figures 7, 8, and 9. Figures 7a₁, 8a₁, 9a₁, 7b₁, 8b₁, and 9b₁ demonstrate the matched feature point pairs, which exhibit consistent slope and distance characteristics. In terms of extracting correct feature point pairs, the KAZE algorithm outperforms the SIFT and SURF algorithms as shown in Table 1. Figures 7a₂, 8a₂, 9a₂, 7b₂, 8b₂, and 9b₂ illustrate the overlap between the first frame mask and the registered transformed second frame masks for SIFT, SURF, and KAZE algorithms respectively. Notably, the KAZE algorithm achieves a remarkable mask overlap rate of 80.85%. It is important to note that these masks represent roads that may enter or exit the field of view during aerial flight; hence they are not completely identical between two images but maintain complex shapes that remain unchanged over time. As two images become more similar in nature, their mask overlap rate increases accordingly. Since there is typically no scenario where multiple transformation matrices correspond to a single overlap rate value. Therefore, it can be utilized as a parameter to measure registration accuracy effectively. Finally, figures 7a₃, 8a₃, 9a₃, 7b₃, 8b₃, and 9b₃ display composite images of different frames after being registered using SIFT, SURF and KAZE algorithms respectively. The registered images appear clearer after undergoing denoising.

Figure  7.  SIFT registration regarding two groups. a₁) matching points in the first group images a₂) mask overlapping of the first group images a₃) registered image of the first group images b₁) matching points in the second group images b₂) mask overlapping of the second group images b₃) registered image of the second group images.

DownLoad: Full-Size Img PowerPoint

Figure  8.  SURF registration regarding two groups. a₁) matching points in the first group images a₂) mask overlapping of the first group images a₃) registered image of the first group images b₁) matching points in the second group images b₂) mask overlapping of the second group images b₃) registered image of the second group images.

DownLoad: Full-Size Img PowerPoint

Figure  9.  KAZE registration regarding two groups. a₁) matching points in the first group images a₂) mask overlapping of the first group images a₃) registered image of the first group images b₁) matching points in the second group images b₂) mask overlapping of the second group images b₃) registered image of the second group images.

DownLoad: Full-Size Img PowerPoint

Table  1.  The first group image registration

Algorithm	Unmatched image	SIFT	SURF	KAZE
Coarse registration	-	47	75	46
Consistent slope registration	-	5	5	6
precise registration	-	2	2	4
P	35.09%	77.88%	78.36%	80.85%

 | Show Table

DownLoad: CSV

The registration results of this study are presented in Table 1. Following image registration, a significant improvement was observed in the mask overlap rate. Notably, the KAZE operator-based registration yielded the most favorable outcome, exhibiting a substantially higher number of matching points and overlap rate compared to SIFT and SURF algorithms. The KAZE algorithm demonstrated superior performance and exhibited heightened robustness.

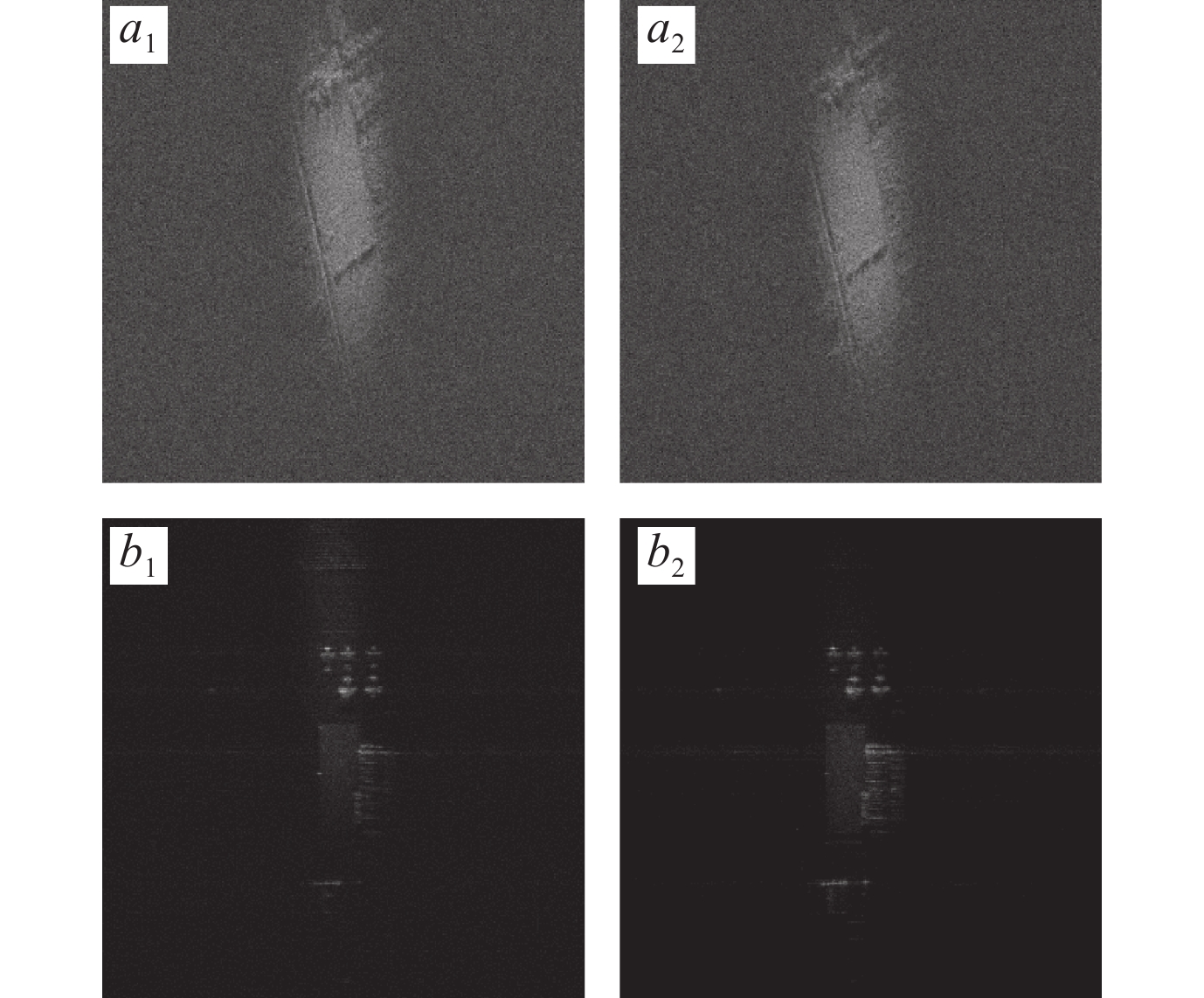
The image is first subjected to Gaussian filtering in order to mitigate noise, followed by normalization of the filtered image as depicted in Figure 10. Directly fusing the images without the registration leads to image blurring.

Figure  10.  Image fusion without registration. a₁) first frame image of first group images a₂) second frame image of first group images a₃) fusion image of first group images b₁) first frame image of second group images b₂) second frame image of second group images b₃) fusion image of second group images.

DownLoad: Full-Size Img PowerPoint

The present article is based on the utilization of SIFT, SURF, and KAZE algorithms for the purpose of image registration and fusion. It can be observed from Figure 11 that the fused image effectively enhances the informational content of the original image. Furthermore, Table 2 demonstrates that the fused image exhibits a higher level of entropy in comparison to its original counterpart. Moreover, it is worth noting that through image fusion, noise reduction within the images can be achieved as evidenced by Table 2 where there is a significant decrease in normalized standard deviation.

Figure  11.  Fusion images. a₁) SIFT registration of first group images a₂) SURF registration of first group images a₃) KAZE registration of first group images b₁) SIFT registration of second group images b₂) SURF registration of second group images b₃) KAZE registration of second group images

DownLoad: Full-Size Img PowerPoint

Table  2.  The second group image registration

Algorithm	Unmatched image	SIFT	SURF	KAZE
Coarse registration	-	77	25	427
Consistent slope registration	-	8	13	21
precise registration	-	3	4	6
P	9.11%	50.74%	53.72%	56.66%

 | Show Table

DownLoad: CSV

Table  3.  The first group image fusion

Algorithm	First frame	Second frame	SIFT	SURF	KAZE
D	27.5213	25.4459	20.3346	20.7207	20.1324
EN	6.4148	6.4108	6.6505	6.6183	6.6187

 | Show Table

DownLoad: CSV

Table  4.  The second group image fusion

Algorithm	First frame	Second frame	SIFT	SURF	KAZE
D	24.4690	24.7786	20.9473	21.1439	20.6527
EN	4.9098	4.9027	5.4411	5.4413	5.4349

 | Show Table

DownLoad: CSV

The standard deviation of the mask in Table 2 represents the normalized gray-level standard deviation within the masked region. The masked region consists of a single land surface type with approximately similar dielectric constants, thus attributing the gray-level standard deviation on its mask primarily to noise interference. A smaller normalized standard deviation indicates reduced image noise. In this article, the term "mask" refers to the overlapping area between the mask of the first frame image and the transformed mask of the registered second frame. The fused image exhibits lower levels of noise compared to its original counterpart, demonstrating that image fusion possesses an inherent capability for noise reduction. Leveraging KAZE algorithm, fused images exhibit minimal noise and enhanced registration accuracy while simultaneously increasing information content.

IV.   Conclusion

The article investigates the registration and fusion methods of terahertz sequence images. In this study, an improved RANSAC algorithm with a forward preprocessing method is developed to address the challenging problem of registering image sequences with strong noise. The KAZE operator demonstrates stronger robustness in the algorithm for registering images with strong noise, resulting in a significantly higher number of correctly matched point pairs compared to SIFT and SURF algorithms, thus making it more suitable for such scenarios. Furthermore, it is demonstrated that image registration and fusion algorithms can enhance the amount of information in an image while reducing image noise.