A Combined Countermeasure Against Side-Channel and Fault Attack with Threshold Implementation Technique

I.   Introduction

As we know, a mathematically secure cryptographic algorithm does not mean it is secure in practice. A lot of implementation attacks have been proposed, among which side-channel attack (SCA) and fault attack (FA) are two main kinds of physical attacks against cryptographic implementations. SCA seeks the information leakage which is correlated with some sensitive information such as the secret key. By exploring the dependence between the information leakage and the sensitive information, the attacker can recover the secret. One of the most popular side-channel information leakage is the power consumption from the cryptographic implementations. In 1999, Kocher et al. proposed differential power attack (DPA) firstly [1]. Since then, various kinds of power attacks have been presented including correlation power attack (CPA) [2], template attack (TA) [3] and so on. Meanwhile, how to efficiently resist the attack is also investigated. Masking technique [4] is one of the most popular countermeasures against SCA from the view of algorithmic level, which includes Boolean masking and multiplication masking. In a Boolean masking scheme, random values are applied exclusive-or operation with some intermediate values during cryptographic operations, which can hide the possible dependence between the side-channel information leakage from intermediate operations and sensitive data. Among Boolean masking schemes, threshold implementation (TI) technique [5] has caused much research attention in recent years. Besides the SCA, the first FA against cryptographic implementation was given by Boneh et al. in EUROCRYPT’97 [6]. After that, FAs against various kinds of cipher schemes were proposed including DES [7], AES [8], DBlock [9], and so on. Infection [10] is one of the most popular countermeasures to resist FA. It requires the redundant computations besides the original ones in the cipher algorithm. The infective countermeasure is realized by scrambling the data paths of the original and redundant computations. The well-designed infection can make the final faulty ciphertext independent from the secret key.

The countermeasures mentioned above only consider single SCA or FA. One of the main drawbacks is, they are easily vulnerable to another attack or combined attack. To defend both SCA and FA, a popular method is to combine the SCA-resistant techniques with the FA-resistant ones. For instance, Private Circuits II is constructed based on Private Circuit I together with the FA-resistant encoding gadget [11], however, it cannot guarantee the security under the glitch environment. In CRYPTO 2016, a combined countermeasure called ParTI was presented which combines the concept of TI with the concurrent error detection techniques [12]. Recently, many designers adopt multi-party computation (MPC) protocols and infective techniques in the combined countermeasures. CAPA takes MPC protocol SPDZ, along with corresponding shared MAC tags [13], it is of formal security, but its resource consumption is too much. M&M achieves an efficient countermeasure with TI and multiplication-based MAC operation [14]. There are also countermeasures that adopt a single technique to resist both SCA and FA. The countermeasure in CT-RSA 2017 achieves the comprehensive resistance with the encoding technique [15]. The one in CHES 2018 takes the MPC based on polynomial to disable SCA and detect the fault injection [16]. To sum up, although some of the protection schemes introduced above have high safety, they have a common shortcoming, namely high resource consumption. In view of this phenomenon, this paper proposes a comprehensive protection scheme with less resource consumption.

Our contributions　In this paper, we present a combined countermeasure scheme which can resist both SCA and FA. Different from the methods mentioned before, we combine the TI technique and exchange-based infection scheme to resist the two attacks. The details are as follows.

1) A combined countermeasure scheme based on TI technique and exchange-based infection is proposed. TI can not only provide protection against power attack, but also can be combined with exchange-based infection to enhance its resistance to FA. The advantage of the proposed countermeasure is the simple structure, which is very friendly for hardware implementation.

2) The security of the scheme is analyzed systematically. The proposed combined countermeasure has at least the same level of SCA-security as a plain d-order TI without FA countermeasures. The scrambled implementation based on duplication structure together with TI provide protection against FA. The scrambled implementation confuses the fault propagation path. TI realizes the segmentation of the original fault value, and the non-complete property of TI makes the information of the original fault value difficult to be obtained by the attacker.

3) Finally, we give a case design for the lightweight cryptographic algorithm LED which can achieve the 1-order SCA security and resist the differential fault attack. Besides, we verified its low overhead and resistance against SCA and FA on SAKURA-X FPGA evaluation board.

II.   Preliminaries

1   Threshold implementation

TI is a popular countermeasure against SCA [5]. It is constructed based on secret sharing and multi-party computation protocols. To resist the $d$th order SCA on the cipher computation $y = f(x)$, the designer should firstly encode the input $x$, then encode the cipher function $f$, and finally decode the output $y$.

Input encoding splits the input $x$ into $S_x$ shares ($x_1,x_2,\ldots,x_{S_x-1},x_{S_x}$) by the means of Boolean masking, $x = \bigoplus_{i = 1}^{S_x} x_i$. To make the input encoding uniform, we can generate $S_x-1$ of these shares with (pseudo) random number generator. Function encoding splits the cipher function $f$ into $S_y$ component functions $f_j$, $j = 1,2,\ldots,S_y$. Each component function takes a subset of $\{x_1,x_2,\ldots,x_{S_x-1},x_{S_x}\}$ as its input. Without loss of generality, we denote ${\boldsymbol{x_j}}$ and $y_j$ as the input and output of $f_j$, respectively. The encoding of cipher function needs to satisfy three properties. The first property is the correctness of the computation. That is, for any value of $x$, $f(x) = \bigoplus_{j = 1}^{S_y} f_j({\boldsymbol{x_j}})$. The second property is the $d$th order non-completeness of the computation. That is, any combination of $d$ component functions $f_j$ should always be independent of at least one input share. The third property is the uniformity of the computation, which means, if the input encoding is uniform, the output shares of all the component functions ($y_1,y_2,\ldots, y_{S_y-1},y_{S_y}$) should also be jointly uniform. The uniformity of computation is necessary when ($y_1,y_2,\ldots,y_{S_y-1}, y_{S_y}$) are used as inputs in further parts of the cipher algorithm. If $f$ is the last part of the cipher algorithm, output decoding reconstructs the output as $y = \bigoplus_{j = 1}^{S_y} y_i$. The uniform input encoding and function encoding make all the available intermediate shares appear with the same probability. Therefore, the average power consumption of TI leaks no information of the original input, which prevents many SCAs, such as CPA and DPA. Besides, the properties of TI also ensure the resistance against d-probing attack [17]. With proper insertion of register in TI circuit, even the presence of glitches does not result in the leakage of information.

The key of TI lies in the function coding. The number of shares required in TI is jointly determined by the order of SCA and the algebraic degree of the cipher function. Reference [18] has proved that for the functions with algebraic degree of $t$, there always exists a $d$th order TI with $S_x$ input shares and $S_y$ output shares, where $S_x\geq d\times t+1$ and $S_y\geq \binom{S_x}{t}$. The linear function $f(x) = ax+b$ in cipher algorithm can be split into a series of component functions, $f_1 = ax_1+b$, $f_j = ax_j$, $j = 2,\ldots,S_y$. Each component function takes one share of $x$ as its input. For the nonlinear function with high algebraic degree, such as S-box, the designer usually decomposes it into a series of cascaded nonlinear operations with low algebraic degree, before constructing component functions for each operation. Note that, it requires additional registers between the cascaded nonlinear operations in TI circuit.

2   Joye exchange scheme

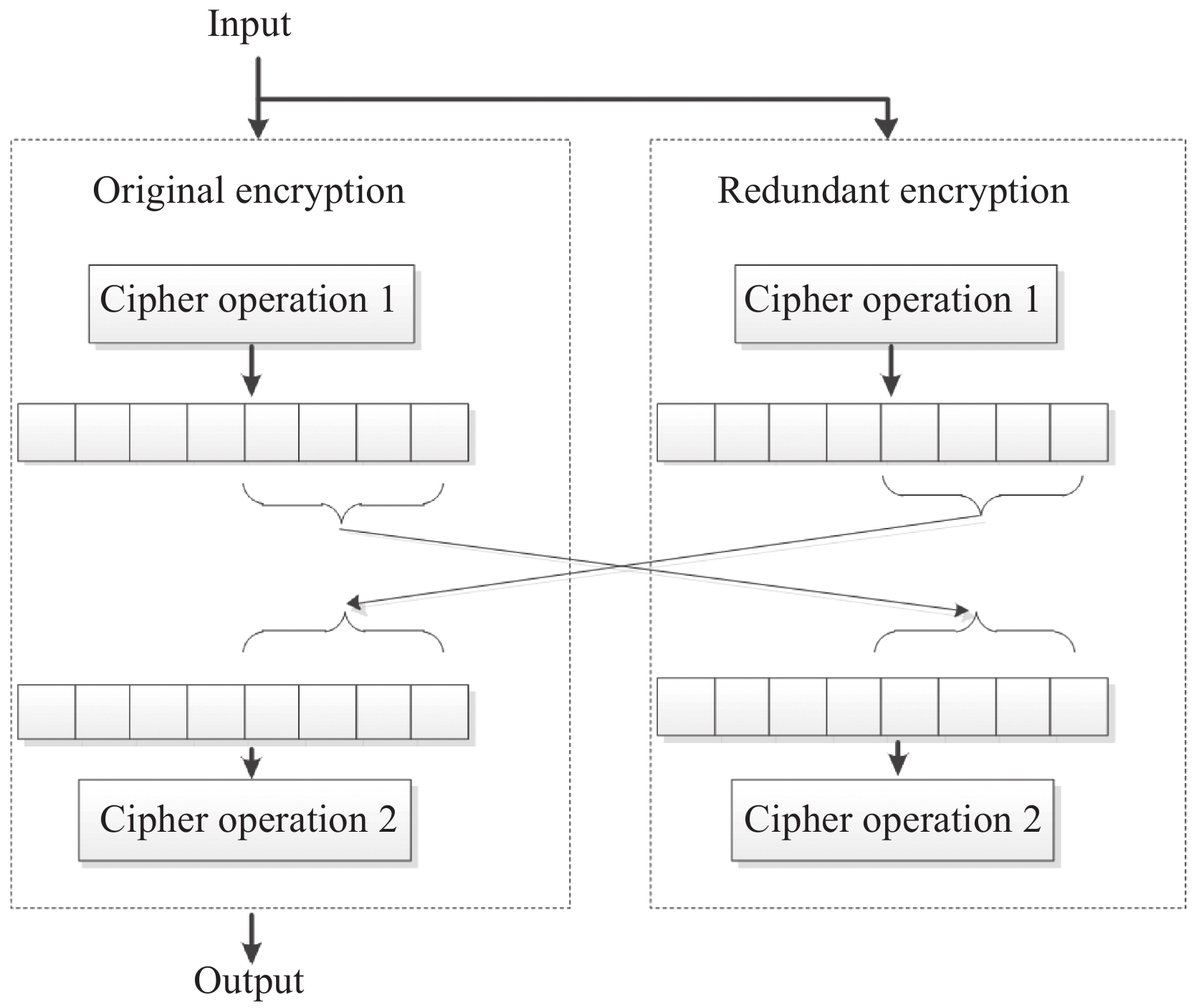
The exchange scheme proposed by Joye et al. is a countermeasure against FA [10]. The main idea is duplicating the cipher implementation, exchanging the original and redundant intermediates during the encryption, and outputting the original encryption result as the final ciphertext. Take the encryption process “cipher operation 1,” and “cipher operation 2” as an example and Fig.1 illustrates it. The exchange is performed between the last 4 bits of the intermediates. Concerning the fault injection on the last 2 bits of the input of the original “cipher operation 1,” after the exchange operation, the faulty bits are swapped with the correct ones. The output ciphertext will not yield the expected fault. The countermeasure can resist FA in a certain extent. However, when the fault is injected in some other part of the input, the output faulty bits remain unchanged. Since no randomness has been introduced to the faulty output, it is still possible to perform the attack [19]. In the following part, we will show how the combination with TI can strengthen the resistance of the exchange scheme against the FA.

Figure  1.  The basic structure of Joye exchange.

DownLoad: Full-Size Img PowerPoint

III.   Framework for the Model

1   Countermeasure description

Our design aims to resist both the SCA and FA. The basic idea is the combination of TI and a special kind of infection scheme. The infection scheme provides the protection on the FA. When a fault is injected, the ciphertext is still outputted, but it has become a random value which can not provide the useful information for the attacker. TI mainly plays the role to resist the power attack. Besides, it also strengthens the resistance against the FA which will be illustrated as follows.

The infection scheme originates from the work of M. Joye in 2007 [10]. In the work, the AES hardware implementation is duplicated and the state bytes are scrambled between the two executions. Such methodology can ensure that a fault on one data path will likely result in a fault on the other data path. So the attacker has difficulty to acquire some knowledge on the fault propagation to succeed in recovering information on the secret key. However, the problem of this methodology is, no randomness is induced into the implementation procedure. So once the attacker knows the fault propagation path, he can also recover the secret key with some more efforts. Our methodology also duplicates the implementation of the cipher, and each path of the cipher is implemented with TI technique. Different from [10], one share or more shares of the state bytes are scrambled between the two executions. By this means, randomness used in TI also helps to confuse the fault propagation. In order to generate the correct ciphertext with no fault injection, the same shared way and random numbers are used in the two data paths.

Next we take a target function $F:F_{2}^{n}\rightarrow F_{2}^{m}$ as an example to illustrate how the scheme works. The algebraic degree of $F$ is $t$. Firstly, $F$ is implemented with $d$-order secure TI. The input $x$ is split into $S_x$ shares which satisfies $x = x_{1} \oplus x_{2} \oplus x_{3} \cdots\oplus x_{S_x}$, and the output $y$ is split into $S_y$ shares which satisfies $y = y_{1} \oplus y_{2}\; \oplus y_{3} \cdots\oplus y_{S_y}$. $y_{i} = f_{i}(x_{1}, x_{2} ,x_{3},\ldots, x_{S_x})$. According to [18], $S_x\geq d\times t+1$ and $S_y\geq \binom{S_x}{t}$.

Besides, there is another redundant TI implementation same as $F$. The input $x'$ is split into $x'_{1}, x'_{2},\ldots, x'_{S_x}$, and the output $y'$ is split into $y'_{1}, y'_{2}, y'_{3}, \ldots, y'_{S_y}$. $y'_{i} = f_{i}(x'_{1}, x'_{2} ,x'_{3} ,\ldots, x'_{S_x})$. If no fault occurs, $x_{i} = x'_{i},0 \leq i \leq S_x$. Then, ${y_{i}}$ and $y'_{i}$ are exchanged in a random way. ${y_{1}, y_{2} ,y_{3},\ldots, y_{S_y}}$ and ${{y'_{1}, y'_{2}, y'_{3}, \ldots, y'_{S_y}}}$ will enter a $G$ transformation function as the input. At the same time, a random vector ${r_{1}, r_{2},\ldots, r_{S_y}}(r_{i}\in{0,1})$ also enters the $G$ function as the input. $G(y_{1}, y_{2}, y_{3}, \ldots, y_{S_y},y'_{1}, y'_{2}, y'_{3},\ldots, y'_{S_y},\, r_{1},\, r_{2},\,r_{3},\ldots, r_{S_y}) = (\neg r_{1}y_{1}\oplus r_{1}y'_{1}, \neg r_{2}y_{2}\,\oplus$$r_{2}y'_{2},\ldots, \neg r_{S_y}y_{S_y}\oplus r_{S_y}y'_{S_y},\, r_{1}y_{1}\oplus \neg r_{1}y'_{1},\, r_{2}y_{2}\oplus \neg r_{2}y'_{2}, \ldots, r_{S_y}y_{S_y}\oplus \neg r_{S_y}y'_{S_y})$. Therefore, whether ${y_{i}}$ and $y'_{i}$ are exchanged depends on the random bit $r_{i}$. The random exchanging way can effectively prevent the adversary from adaptively choosing the next fault injection position. The basic structure is illustrated by Fig.2.

Figure  2.  Basic structure of the combined countermeasure.

DownLoad: Full-Size Img PowerPoint

Let $w = HW(r_{1}, r_{2},r_{3},\ldots, r_{S_y})$ and HW means the hamming weight. In order to fully utilize the incomplete property of TI, $w\leq d$ should be satisfied. The following security evaluation shows that it is helpful to enhance the resistance against fault attack.

For a multi-output Boolean function $F:F_{2}^{n}\rightarrow F_{2}^{m}$, the minimum width of exchanged output is required to be $m$, and the indexes of the exchanged shares for each function are required to be the same. Otherwise, the incompleteness property of TI would be possibly destroyed. For simplicity, we suggest the width of exchanged output bits for each operation layer (e.g., S-box layer) is the block size of the cipher. In the following case design for the 64-bit LED cipher, the swapping width is set to be 64.

2   Security evaluation

1) Attack model

SCA model　The first model we consider is the d-order probing attacks [17]. In this model, the adversary can observe at most $d$ wires of the circuit within a certain time period. The probes the attacker can control during the probing are at most $d$. Moreover, the attacker can not remove the probing position adaptively within a short time.

The second model considers the attacker has the ability to collect power supply signal. He can obtain the power consumption of the whole encryption procedure. By analyzing the dependence of the power consumption on the encrypted data, he can recover the secret data. A $d$-order attack means the attacker can apply the non-linear combination on the obtained power consumption of the intermediate values and recover the secret information. The traditional power attacks under such model include DPA, CPA and so on.

FA model　In this paper, we mainly consider the most popular fault attack, i.e., Differential fault attack (DFA) [7], [8]. It is based on the concrete faulty output value. Under such attack, both correct encryption execution and wrong execution are needed. By exploring the statistical correlation between the faulty values and the correct ones, the attacker can recover the secret information.

2) SCA evaluation

In our scheme, both the original encryption and the redundant encryption are implemented with TI technique. According to the security property of TI, the two encryption path implemented with the $d$-order TI can resist $d$-order probing attack and $d$-order SCA(such as DPA/CPA).

Next we consider the resistance ability of the exchange operation. Generally, the hardware logic of exchange operation is very simple. Hence, the power leakage is hard to be utilized by the attacker. Here we consider the worst case, in which the power consumption of exchanged $w$ components can be acquired by the attacker. It is a linear operation, and will not damage the incomplete property of TI. The information of d components is independent of the original intermediate value, so it can also resist the d-order DPA/CPA.

3) FA evaluation

Here we will illustrate the resistance against DFA. The protection against the DFA is derived from both the scrambled implementation based on duplication structure and TI. As described in [10], the scrambled way helps to confuse the fault propagation path. But it is not enough. The following fault analysis on the countermeasure shows that, once the attacker knows the scrambled way, he can also deduce the fault propagation path and then recover secret key. The reason why the attacks can work is that no randomness is induced in the countermeasure. Our countermeasure can overcome the weakness because randomness is induced in the TI, which can also help to confuse the fault value. Moreover, the information of the fault value is also spitted by the shared structure. The non-complete property of TI ensures the whole information of the fault value cannot be obtained by the attacker.

As we know, the implementation of the last round is the most difficult to defend DFA because of the worst diffusion effect when faults are injected in the last-round encryption. So we focus on illustrating the protection effect of last round. Without loss of generality, here we focus on the last TI-target function where the ciphertext will be outputted after the output of function is Xored the round key, which is illustrated by Fig.3.

Figure  3.  The structure of the last-round TI encryption.

DownLoad: Full-Size Img PowerPoint

Denote $C$ as the ciphertext, $C = C_{1}\oplus C_{2}\oplus C_{3}\oplus \cdots \oplus C_{S_{y}}$, $C_{i} = z_{i}\oplus K_{i}$, $K = K_{1}\oplus K_{2}\cdots K_{S_{y}}$, $z_{i} = G_i (y_{1},\ldots, y_{S_{y}},y'_{1},\ldots, y'_{S_{y}},r_{1},r_{2},\ldots, r_{S_{y}})$. When the encryption is correctly executed, $x_{i} = x'_{i}$, So $C = C_{1}\oplus C_{2}\oplus\cdots \oplus C_{S_{y}} = z_{1} \oplus z_{2}\oplus\cdots \oplus z_{S_{y}} = y_{1}\oplus y_{2}\oplus\cdots \oplus y_{S_{y}}$=$y'_{1}\oplus y'_{2}\oplus \cdots \oplus y'_{S_{y}}$.

When a fault is injected into some intermediate round, after the propagation of the fault, the corresponding last-round intermediate values would change into other new values. We denote the new values by $\hat{x} = \hat{x_{1}}\oplus \hat{x_{2}}\oplus \cdots \oplus\hat{x_{S_{x}}}$, $\hat{x'} = \hat{x'_{1}}\oplus \hat{x'_{2}}\oplus \cdots \oplus\hat{x'_{S_{x}}}$, $\hat{y} = \hat{y_{1}}\oplus \hat{y_{2}}\oplus \cdots \oplus\hat{y_{S_{y}}}$, $\hat{y'} = \hat{y'_{1}}\oplus \hat{y'_{2}}\oplus \cdots \oplus\hat{y'_{S_{y}}}$, $\hat{C} = \hat{C_{1}}\oplus \hat{C_{2}}\oplus \cdots \oplus\hat{C_{S_{y}}}$. Let $\hat{x} = x\oplus e_{1}$, $\hat{x'} = x'\oplus e_{2}$. Next we illustrate the resistance against the attack considering different cases of $e_{1}$, $e_{2}$ as follows.

Case 1　Only one of $e_{1}$ and $e_{2}$ equals 0. Here assume $e_{1}\neq0$, $e_{2} = 0$. So $\hat{y'} = y' = C\oplus K$. This usually happens when faults are induced into low-round encryption where the faults are hardly diffused through the swapping operations. For example, a fault is directly injected into $x_{i}$ which is the ith share of $x$. In this case, let us look at the value of $C$. If $\hat{C} = C$, which means the fault has been thrown away by the last swapping operation and the ciphertext is correctly outputted. So the DFA is ineffective. Otherwise, if $\hat{C}\neq C$, there are also two cases. One is when $\hat{C} = \hat{y}\oplus K$, DFA works and the security level equals the plain implementation without any countermeasure. When $\hat{C}\neq \hat{y}\oplus K$, this means some shares of $\hat{y}$ which correlate to $e_{1}$ do not join the final Xor-operation to compute $\hat{C}$. Meanwhile, some other shares of $\hat{y}$ which correlate to $e_{1}$ join the final Xor-operation. Without loss of generality, assume $\hat{y_{1}}$ does not involve the computation of $\hat{C}$ while other shares do. $\hat{y_{1}}$ and at least one of the other shares correlate to $e_{1}$ (here assume $\hat{y_{2}} , \hat{y_{3}}, \ldots, \hat{y_{t}}, t < s_{y}$), so $\hat{C}\oplus K = \hat{y_{2}}\oplus \hat{y_{3}}\cdots\oplus\hat{y_{t}}\cdots\oplus\hat{y_{s}}\oplus \hat{y'_{1}}$ = $\hat{y_{2}}\oplus\hat{y_{3}}\cdots\oplus\hat{y_{t}}\oplus\hat{y'_{t+1}}\oplus \hat{y'_{t+2}}\oplus\cdots\oplus\hat{y'_{s_{y}}}\oplus\hat{y'_{1}}$ = $\hat{y_{2}}\oplus \hat{y'_{2}}\oplus \hat{y_{3}}\oplus \hat{y'_{3}}\cdots\oplus\hat{y_{t}}\oplus\hat{y'_{t}}\oplus \hat{y'}$ = $C\oplus K \oplus \hat{y_{2}}\oplus \hat{y'_{2}}\oplus\hat{y_{3}} \oplus \hat{y'_{3}}\cdots\oplus \hat{y_{t}}\oplus\hat{y'_{t}}$.

As we know, $\hat{y}\oplus \hat{y'} = (\hat{y_{2}}\oplus \hat{y'_{2}}\oplus\hat{y_{3}}\oplus \hat{y'_{3}}\cdots\oplus\hat{y_{t}}\oplus \hat{y'_{t}})\oplus(\hat{y_{1}}\oplus \hat{y'_{1}})\oplus (\hat{y_{t+1}}\oplus \hat{y'_{t+1}})\oplus \cdots (\hat{y_{s_{y}}}\oplus\hat{y'_{s_{y}}})$. Because the TI scheme has secret-sharing property, $(\hat{y_{2}}\oplus \hat{y'_{2}}\oplus \hat{y_{3}}\oplus \hat{y'_{3}}\cdots\oplus\hat{y_{t}}\oplus\hat{y'_{t}})$ is independent from $\hat{y}\oplus \hat{y'}$. So $\hat{C}$ can be regarded as a random mask value Xored with $C$. The attacker can not utilize the value of $\hat{C}$ to reveal the key. Therefore, it is secure against DFA.

Case 2　$e_{1}\neq0$ and $e_{2} \neq 0$. This means the injected faults have been diffused to the last round. Assume $e$ is the original injected fault value. Apparently, both $e_{1}$ and $e_{2}$ are generated from $e$ and some random values after TI function and swapping operations. So $e_{1}$ and $e_{2}$ can be seen as two independent random mask values. Let $m_{1} = y\oplus\hat{y}$. Apparently, $m_{1}$ is also random. If $\hat{C} = \hat{y}\oplus K$, $\hat{C} = y\oplus K\oplus m_{1} = C\oplus m_{1}$. So $\hat{C}$ is random. The similar conclusion holds when $\hat{C} = \hat{y'}\oplus K$.

If $\hat{C}\neq \hat{y}\oplus K$ and $\hat{C}\neq \hat{y'}\oplus K$, $\hat{C}$ is the Xored result respectively from some shares of $\hat{y}$ and $\hat{y'}$. Without loss of generality, assume $\hat{C}\oplus K = \hat{y_{1}}\oplus \hat{y_{2}}\cdots \oplus \hat{y_{t}}\oplus \hat{y'_{t+1}}\oplus \hat{y'_{t+2}}\cdots \oplus \hat{y'_{s_{y}}}$ = $y_{1}\oplus y_{2}\cdots \oplus y_{t}\oplus \hat{y_{1}}\oplus \hat{y_{2}}\cdots \oplus \hat{y_{t}}\oplus y'_{t+1}\oplus y'_{t+2}\cdots \oplus y'_{s_{y}}\oplus \hat{y'_{t+1}}\oplus \hat{y'_{t+2}}\cdots \oplus \hat{y'_{s_{y}}} \oplus y_{1}\oplus y_{2}\cdots \oplus y_{t}\oplus$ $y'_{t+1}\oplus y'_{t+2}\ldots \oplus y'_{s_{y}}$. Let $m_{2} = y_{1}\oplus y_{2}\cdots \oplus y_{t}\oplus \hat{y_{1}}\oplus \hat{y_{2}}\cdots \oplus \hat{y_{t}}$, $m_{3} = y'_{t+1}\oplus y'_{t+2}\cdots \oplus y'_{s_{y}}\oplus \hat{y'_{t+1}}\oplus \hat{y'_{t+2}}\cdots \oplus \hat{y'_{s_{y}}}$, then $\hat{C} = C\oplus m_{2}\oplus m_{3}$. Because $m_{2}$ and $m_{3}$ are respectively independent from $y \oplus \hat{y}$ and $y' \oplus \hat{y'}$, $m_{2}$ and $m_{3}$ are random. So $\hat{C}$ is random and secure against DFA.

From the above security illustration, we can see that, in most cases the scheme is secure against DFA with the help of swapping operation and the TI scheme. However, it can not ensure a perfect protection with probability 1. Some cases will still happen when a fault is induced into low-round encryption and the swapping operation does not change the fault propagation path. The probability of such cases can be effectively reduced by the random swapping operation because the attacker can not get the same ciphertext when the injection condition remains unchanged. Moreover, some penalty functions can also be added to the last-round encryption to further improve the case. In the following countermeasure design of LED, we will design a penalty function with a S-box function and its inverse function. For the case that S-box and inverse S-box are not implemented simultaneously, the Feistel structure with S-box as nonlinear component can be used to extend it.

In this paper, we mainly consider the most popular fault attack-DFA, which utilizes the concrete faulty values of ciphertext to launch the attack. For other faulty value-based attacks such as algebraic fault attack [20], our countermeasure has the similar resistance ability because the ciphertexts are randomized by the infective and TI scheme. However, for those FAs which do not care the concrete faulty ciphertexts, our countermeasure maybe not be applicable. Take the statistical infective fault attack as an example [21], it has been shown neither TI [22] nor infective scheme can resist such attack [21], so our scheme can not resist this attack. More protection requirements mean more resource consumption. In a resource-constrained environment, it is a reasonable strategy to mainly consider the protection for DFA, which is one of the most common and powerful FA methods.

IV.   Case Study

1   The LED cipher

LED is a lightweight block cipher proposed in $2011$ [23]. The block size is $64$ bits, and the key size is $64/128$ bits. The round number is respectively $32$ and $48$. In this paper, we only consider the LED-64 cipher with $64$-bit key size and $32$ rounds.

LED-64 adopts SPN structure. The whole encryption contains round key addition (AddRoundKey) and STEP operation. The intermediate state is a $4\times4$ matrix with $16$ nibbles. Firstly, the round key is Xored with the plaintext, then followed by $8$ STEP operations. Each STEP operation is composed by four identical round operations and AddRoundKey. Each round contains AddConstants, SubCells, ShiftRows and MixColumnsSerial.

AddConstants respectively adds $16$ constants to each nibble of the state with bitwise Xor operation. SubCells apply the non-linear function S-box to the state. ShiftRows shift each row of the state with offset. MixColumnsSerial apply linear matrix operation on all the columns of the state.

There is no key schedule for LED-$64$. The main key $K$ is the round key.

2   Countermeasure design

As introduced in Section III.1, the whole implementation structure of LED-$64$ has two same encryption paths, which are respectively called original encryption and redundant encryption. Each encryption path is implemented with TI technique. S-box is the only non-linear component of LED-$64$. It can be implemented by two cascade functions $G$ and $F$ with degree 2. According to the TI property, at least 3 shares are required to ensure 1-order security against SCA. Here we adopt a 3-share TI technique. Fig.4 illustrates the structure.

Figure  4.  The countermeasure structure of the LED-64.

DownLoad: Full-Size Img PowerPoint

The swapping way of two paths for each encryption is different. The random numbers which control the exchanged way is generated before each encryption starts. In order to save random numbers, the exchanged way for each round remains the same once the random number is generated at the beginning. Because the security target is $1$-order secure, the number of exchanged shares is 1. For example, as illustrated in Fig.4, the third share component is exchanged. The bit width of exchanged component is the block size $64$. The detailed TI design for each encryption component is as follows.

AddRoundKey & AddConstants The round key and constants are only added into one share of intermediate state, which can also ensure the output uniformity and 1-order non-complement property.

ShiftRows The shift operation is respectively applied on each share component. Because the hardware logic is very simple and can be implemented by changing the connecting way, it is omitted in Fig.4.

SubCells LED-64 uses the same 16 4×4 S-boxes of PRESENT. In order to obtain secure TI implementation of S-box with low cost, we adopt the same decomposition way of S-box and TI implementation way as [24]. The decomposition way is as follows:

where $x$ and $a$ are the most significant bits of S-box input and output. The threshold implementation way is as follows:

The index $i = 1,2,3$ and the index addition is modulo 3. Here the S-boxes are implemented parallelly.

MixColumnsSerial The column mixture operation is respectively applied on each share component.

Besides the normal encryption, in order to further strengthen the FA resistance for last-round encryption, we add the inverse function $F^{-1}$ and $G^{-1}$ to increase the exchange times.

After the normal encryption, each path will execute $G$, $F$, $F^{-1}$ and $G^{-1}$ which is also implemented with TI. Exchange operation is also applied after each function. Finally, all the share components of the original path will be combined and outputted as ciphertext.

The TI designs of $F^{-1}$ and $G^{-1}$ are similar to $G$, $F$ which adopt cycle decomposition mode.

3   Hardware implementation

The random number overhead of the countermeasure contains two parts: the ones required for threshold implementation and the ones needed for the share exchange. The 1-order TI of LED contains 3 shares and 16 S-boxes which are parallelly implemented, so it requires $64\times (3-1) = 128$ bits random numbers in each encryption. As for share exchange, it requires $\lceil\log_2 3\rceil = 2$ bits random numbers to decide which share to exchange. Overall, each combined countermeasure requires only 130 bits randomness, which is 1.015 times as large as that required in a single SCA countermeasure.

In LED implementation based on the countermeasure prototype, the encryption requires 64 clock cycles, which is the same as that required in a single SCA countermeasure. As for the improved implementation, it requires four additional clock cycles to complete the encryption, which has little impact on the throughput.

In terms of the hardware overhead of protection, the redundant encryption doubles the circuit area. The share exchange operation between $x$ and $x'$ can be implemented with Not ($\neg$), And ($\cdot$) and Xor ($\oplus$) operations simply as $y = (r\cdot x) \oplus ((\neg r)\cdot x')$ and $y' = ((\neg r)\cdot x) \oplus (r\cdot x')$, where $y$ and $y'$ denote the outputs. $r$ is the random bit that controls the exchange. Therefore, the share exchange operations have no significant effect on the circuit area. We synthesize the 1st-order countermeasure prototype with the ASIC component library UMC 0.18 μm [25] and summarized the implementation overhead in Table 1. It requires 18.47 kGE in total. The S-box and inverse S-box used in the improved countermeasure will require little additional cost of area by reusing the ones in encryption part and decryption part.

Table  1.  Cost of the 1st-order FA-SCA countermeasure for LED

	Area(kGE)	Latency(clock cycle)
States, keys and constants storage	4.32	0
MixColumns	3.08	0
SubCells	8.19	2
Others	2.88	0
In total	18.47	64

 | Show Table

DownLoad: CSV

In order to compare our FA-SCA resistant countermeasure with the existing ones, we focus on the 1st-order implementations and list their area overheads. To minimize the effects of different synthesis libraries and different cipher algorithms in area, we refer to [14] and use the overhead factor to make the comparison. The overhead factor is the ratio of the FA-SCA countermeasure overhead to the SCA-only countermeasure overhead.

As shown in Table 2 [12]–[14], [25]–[28], our countermeasure has the minimum overhead factor. It is a compact countermeasure to resist both SCA and FA.

Table  2.  Area comparison between the 1st-order FA-SCA countermeasures

Countermeasure	Cipher	Synthesis library	SCA-only (kGE)	FA-SCA (kGE)	Overhead factor
TI+PCII [26]	PRESENT	−	−	−	$\geq 10$
CAPA [13]	KATAN	Nangate 45 nm [27]	3.6	30.5	8.47
ParTI [12]	LED	UMC 0.18 μm [28]	7.9	20.2	2.56
M& M [14]	AES	NanGate 45 nm [27]	7.6	19.2	2.53
This paper	LED	UMC 0.18 μm [25]	8.0	18.47	2.31

 | Show Table

DownLoad: CSV

4   SCA evaluation

To evaluate the resistance of our countermeasure against SCA, we implement the protected LED encryption on Xilinx Kintex-7 FPGA of SAKURA-X board. To avoid the optimizations in the synthesis step break the non-completeness of the countermeasure, we disable the optimization option and keep hierarchy of the design. In the experiment, we make encryption with a slow clock rate (3 MHz) and sample the power traces at a rate of 500 MS/s. Then we perform SCA evaluation with the test vector leakage assessment (TVLA) technology [29]. The assessment takes the $t$-test statistic ($t$-value) to evaluate the consistency of two groups in power trace distribution, and indicate the SCA leakage of the implementation. Under the confidence level of $99.9995\%$, it takes $\pm 4.5$ as the leakage threshold. If the 1st-order $t$-value exceeds the threshold, the implementation may be vulnerable to the 1st-order SCA. Refer to [30] for the $t$-value calculation and high-order leakage assessment.

To show the effectiveness of the countermeasure, we first disable the PRNG of the implementation and make assessment on the unprotected LED. Here, the power traces are collected within the first 2 rounds’ encryption, which takes 4 clock cycles. After 2500 times encryptions in each group, Fig.5 summarizes the 1st/2nd/3rd-order $t$-test statistics of the unprotected encryptions. Evidently, SCA leakage exists in every order of assessment. Then we turn on the PRNG for the uniform sharing and conduct the protected encryptions for 40M times. Fig.6 shows the corresponding results. As expected, the LED implementation based on the 1st-order TI can prevent at least the 1st-order SCA leakage.

Figure  5.  The $t$-test results of the unprotected LED.

DownLoad: Full-Size Img PowerPoint

Figure  6.  The $t$-test results of the protected LED.

DownLoad: Full-Size Img PowerPoint

5   FA evaluation

In this section, we focus on the DFA-like attacks that rely on the concrete faulty ciphertexts, and work out how the protected LED can randomize the output.

To achieve this goal, we simulate the repetitive fault injections in the protected LED, and make a statistic analysis on faulty ciphertexts. To be specific,

1) Encrypt the same plaintext for $N$ times. Update the input sharing with fresh random number before each encryption.

2) Select a target intermediate share and a fault value. In each encryption, introduce the fault value into the target intermediate share through Xor operation, in order to simulate the repetitive injections with the same fault.

3) Compute the appearance frequency of each faulty ciphertext value in nibble. Then show the randomness of faulty ciphertexts in terms of entropy.

The evaluation focus on the improved LED implementation which adopts 4 extra non-linear operations $G$, $F$, $F^{-1}$, and $G^{-1}$, and 4 extra exchange operations. According to [31], the fault should be injected no later than the last non-linear encryption operation and last AddRoundkey of LED. Therefore, there exist at least 5 exchange operations between the fault injection and the ciphertext output. For each selected fault injection scenario, we repeat the encryption for 500,000 times and show the randomness of the ciphertext nibbles in Table 3. In this table, the entropy 0 means the fault does not propagate to the nibble. It has no effect on the FA-resistance of LED. The entropy of faulty nibbles is close to 4 bit in all scenarios. It means that improved countermeasure can greatly randomize the faulty ciphertext and resist DFA-like attacks.

Table  3.  The randomness of ciphertext nibbles in the improved LED implementation

Injection target	Entropy of 16 ciphertext nibbles
Input of the last round $F$ (5 exchanges)	3.878, 3.789, 3.870, 3.857, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
Input of the last round $G$ (6 exchanges)	3.951, 3.950, 3.969, 3.962, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
Input of the penultimate round $F$ (7 exchanges)	3.992, 3.994, 3.993, 3.994, 3.993, 3.993, 3.993, 3.990, 3.995, 3.992, 3.993, 3.993, 3.993, 3.994, 3.995, 3.992
Input of the penultimate round $G$ (8 exchanges)	3.999, 3.998, 3.998, 3.998, 3.998, 3.998, 3.998, 3.998, 3.999, 3.998, 3.999, 3.999, 3.998, 3.998, 3.999, 3.998

 | Show Table

DownLoad: CSV

V.   Conclusions

In this paper, we propose a countermeasure which combines TI and Joye exchange scheme. TI technique ensures it is provable secure against SCA. Joye exchange scheme was originally proposed to resist the FA by changing the executing path. However, if the exchanging way is determined, the attack can still guess the fault propagation path and break the countermeasure with some more efforts. Our scheme can strengthen the fault attack ability by exchanging the encryption components in a random way which increase the guess difficulty for the attacker. Moreover, TI diffuses the injected fault into some share components. The incomplete property ensures the original injected fault is independent from the final fault value. Therefore, TI also helps to increase the resistance against fault attack.

Based on the scheme, we also design a case countermeasure for the lightweight block cipher LED-64. According to the S-box property, we design a 3-share based scheme and each time only one share is exchanged. We also implement it in the FPGA evaluation board SAKURA-X. The hardware evaluation shows it has low cost compared with other methods. Besides, we apply the TVLA method to evaluate the resistance against SCA and can not find the 1-order sensitive information leakage. For the FA, the entropy of faulty ciphertext is near to 4, so the faulty ciphertext can be seen as random which means it is secure against faulty value based attack.